Calculated items reference

Calculation in boards

This reference guide is for calculated items. Calculations in boards has it's own guide and is used inside the product with access to additional functions.

Calculated items take a set of variables, applies an aggregation to each of the input variables to align them in time and finally applies a formula that returns a single value for each timestamp. If we break this down, we can start defining what a calculated item will look like.

Requirements

To create a new calculated item, you will need to be an administrator of your organization.

A calculated item contains three basic components, a set of variables, a formula and an aggregation setting.

Variables

The input to a calculated item is its variable(s), where each variable is an existing item in Clarify, these provide us with the data to perform the calculation on. When we choose the items we want to use, each one gets assigned a variable name that we can use when referring to it in our formula.

Aggregation

The aggregation for a calculated item is applied to all the variables, and is defined by a time period, and an aggregation method. Examples of this could be sum(1 hour) or average(15 minute).

When we perform our calculation, we will take the value of each variable, at each available timestamp, as input. Since items don't necessarily have timestamps that are exactly the same, let's consider what would happen both when they do and when they don't.

Timestamps exactly overlap

For items where the timestamps perfectly overlap, there is no need to aggregate the data before performing calculations. We simply want to take the value of each item, at each timestamp, and perform our calculation.

What to do when you don't need aggregation

When defining calculated items in Clarify, you need to specify an aggregation. But what should we do in cases where we know that the timestamps align, and we want to preserve the original resolution of the data? In these cases, we can simply set the aggregation to be a higher resolution than the original data.

As an example, if you want to add together two items where values are stored once per hour, setting the aggregation time to once per minute will result in keeping the original resolution.

Timestamp overlap exactly

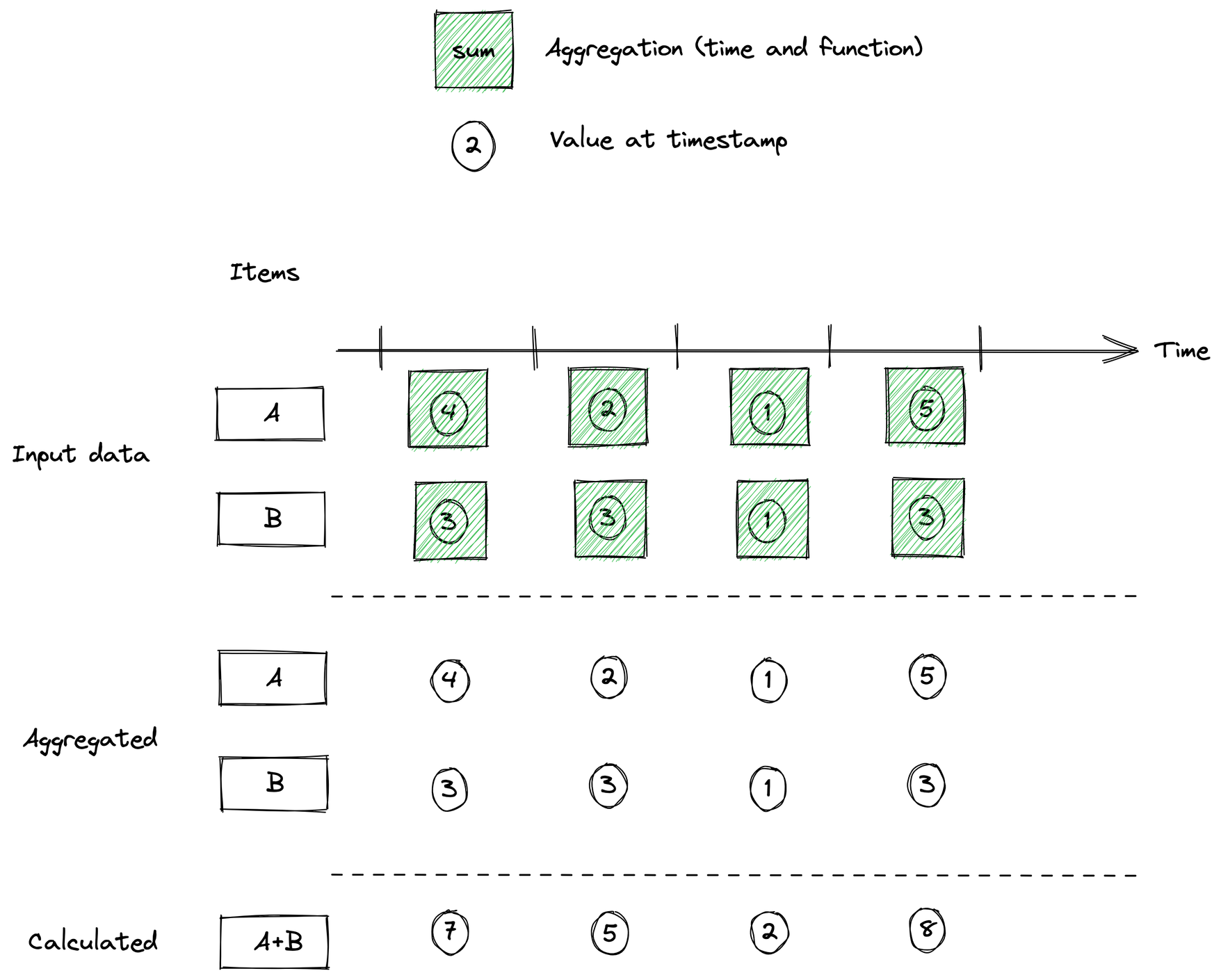
Timestamps don't overlap

If the timestamps don't overlap we can use aggregation to re-align them in a way that makes us able to perform the calculation we want.

Timestamp don't overlap

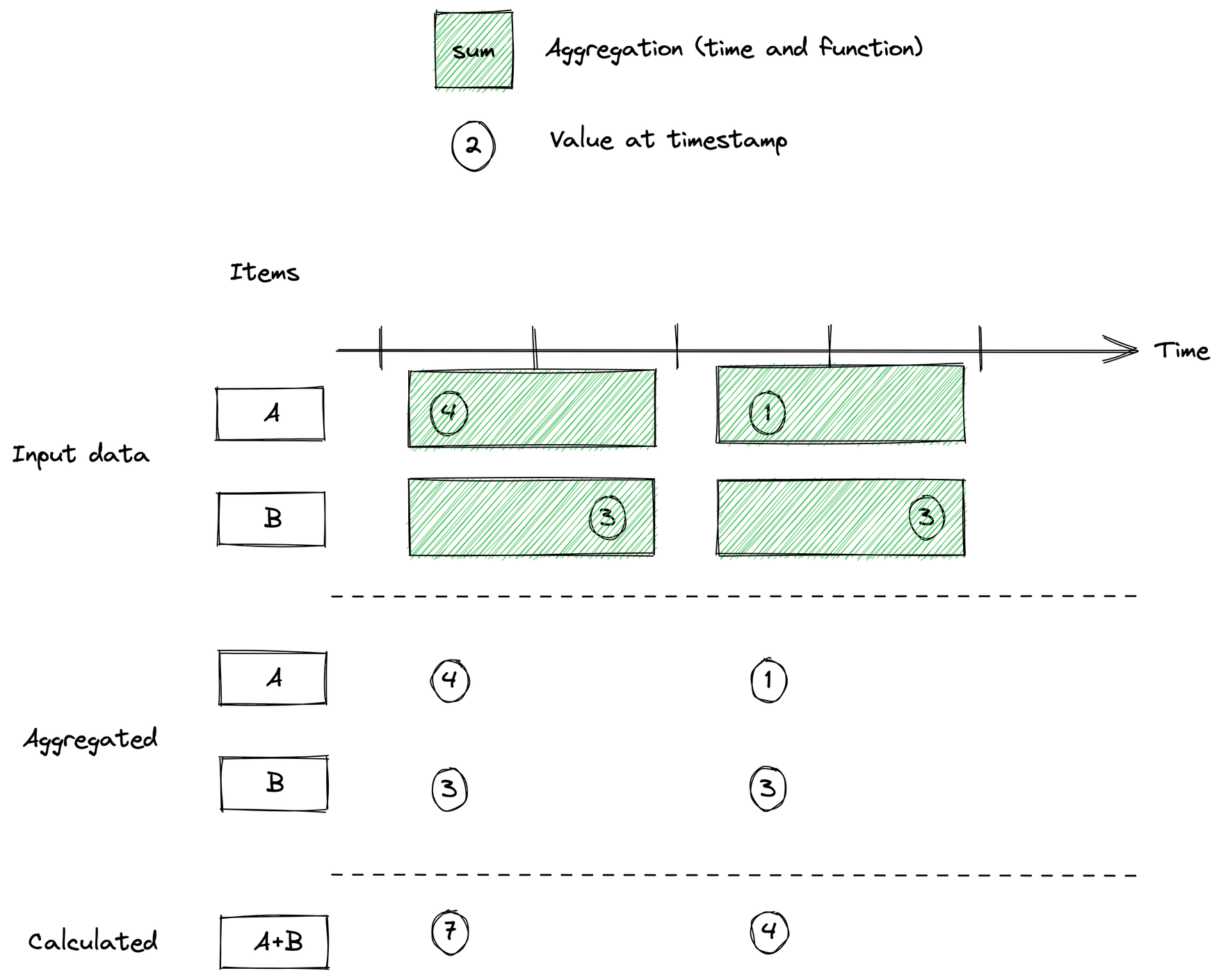
Let's also consider one last case that we can use aggregation time for, which is down-sampling our data prior to performing calculations. This happens if we set the aggregation time high enough that it covers more than one sample for each variable. In that case, multiple samples for each variable will be aggregated together, and the result of that will be used for the calculation.

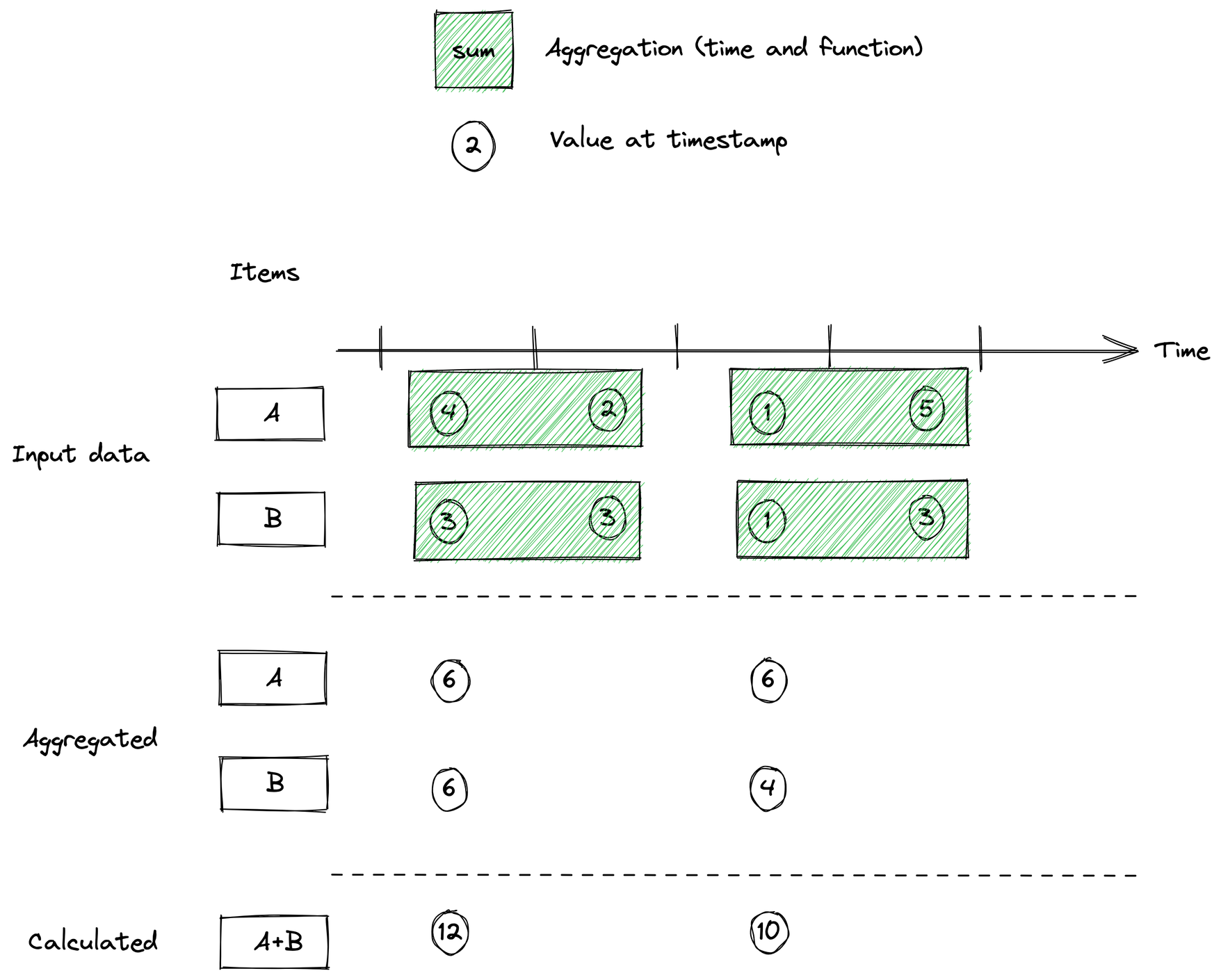
Formula

The formula tells Clarify what to do with the values for each time stamp after the aggregation step.

Mathematical operations

For mathematical operations, the following operators are currently supported:

• + - addition
• - - subtraction
• * - multiplication
• / - division
• ** - power of

Aggregation:

• count(...) - The number of non-empty inputs for all timestamps where there is at least one non-empty input.
• min(...) - minimum of all non-empty inputs for all timestamps where where there is at least one non-empty entry.
• max(...) - maximum of all non-empty inputs for all timestamps where where there is at least one non-empty entry.
• sum(...) - sum of all non-empty inputs for all timestamps where there is at least one data non-empty entry.
• avg(...) - average of all non-empty inputs for all timestamps where where there is at least one non-empty entry.

Trigonometry:

• sin(x) - sine
• sinh(x) - hyperbolic sine
• asin(x) - arcsine / inverse sine
• asinh(x) - hyperbolic arcsine
• cos(x) - cosine
• cosh(x) - hyperbolic cosine
• acos(x) - arccosine / inverse cosine
• acosh(x) - hyperbolic arccosine
• tan(x) - tangent
• tanh(x) - hyperbolic tangent
• atan(x) - arctangent / inverse tangent
• atanh(x) - hyperbolic arctangent
• atan2(x,y) - arctangent of two numbers / four-quadrant inverse tangent

Rounding:

• round(x) - round to nearest integer
• floor(x) - round down to closest integer
• ceil(x) - round up to closest integer

Error function:

• erf(x) - the (Gauss) error function
• erfinv(x) - the inverse of the (Gauss) error function
• erfc(x) - the complimentary (Gauss) error function
• erfcinv(x) - the inverse of the complementary (Gauss) error function

Other math functions:

• sqrt(x) - square root
• log(x) - the natural logarithm of x
• log1p(x) - the natural logarithm of 1+x with higher precision for small values of x
• log2(x) - the base 10 logarithm of x
• log10(x) - the base 10 logarithm of x
• gamma(x) - the Gamma function

Time functions

A single time function is available to calculated items:

• time_seconds() - return the number of seconds since the UNIX epoch with floating point precision

Note that in calculated items the time_seconds() function only return a result when at least one other item contains a value. This is different from how it works for the clarify.evaluate API call and for calculations in Boards.

Conditional

We also support conditional operations, and a ternary syntax which supports nesting for fine-grained control over evaluation:

• <condition> ? <if true> : <if false> - ternary condition
• <condition> ? <if true> - ternary condition with only if true parameter
• <condition> ? - ternary condition without any parameters; return 1 if true or 0 if false.
• <value> ?? <if null> - null coalesce function; replace omitted (NULL) values with if value.
• == - equality
• && - and
• || - or
• > - larger than
• < - smaller than
• >= - larger than or equal
• <= - smaller than or equal

By default, division and multiplication is evaluated before addition and subtraction. To explicitly control the order of evaluation, you use parenthesis.

Example formulas

• Add together three variables a + b + c.
• Calculate average of two variables (a + b) / 2
• Multiply by a constant a * 10
• Calculate a to the power of 2 a**2
• Calculate a complicated KPI sqrt(a) + (b / (d * 2))
• Compare two variables and return the lowest a < b ? a : b
• Compose multiple conditions to create an enum a > 10 ? (a > 20 ? 2 : 1) : 0
• Check if a is equal to 10, if is return 1, otherwise return 0 a == 10 ? 1 : 0
• Check if a is larger than b, if so return a, otherwise return b a > b ? a : b
• Check if a is larger than 10, if so check if it's also larger than 20. If larger than 20, return 2, if larger than 10 return 1, otherwise return 0 a > 10 ? (a > 20 ? 2 : 1) : 0
• Check if a is larger than 5 and b is equal to 2, if so return true, otherwise return false a > 5 && b == 2

Constants

The following constants can be used in calculations. Constants use capital letters and have 62 significant digits.

• E - Euler's number
• PI - Archimedes's constant
• PHI - The golden ratio

Omitted values

Breaking change

On 2023-08-25 we deployed a deliberate breaking change that alters the omit handling for the add (+) and subtract (-) operators.

Even with aggregation there will be cases where not all variables in a calculation will have values at every timestamp. In these situations, it's important to understand what Clarify will do with the output values.

Clarify standard operators only produce a result when both inputs are present. In other words, if at least one of the input values are omitted, the result wil be omitted as well. In addition, operations that returns undefined results, such as divisions by zero, will return omitted values as well. We do however allow operations to combine values with omitted values by using either ternary conditions or the sum function.

Below is a list of the potential situations that can arise, as well as the result that will be returned.

• 0 / 0 = omitted
• omitted / X = omitted
• X / 0 = omitted
• X / omitted = omitted
• X * omitted = omitted
• X + omitted = omitted
• X - omitted = omitted
• omitted + X = omitted
• omitted - X = omitted
• X == null ? X : 0 return 0 if X is omitted.
• sum(omitted, omitted) = omitted
• sum(X, omitted) = X
• sum(omitted, X) = X
• sum(omitted, -X) = -X
• sum(omitted, X, Y) = X+Y
• count(omitted, X, Y) = 2
• avg(omitted, X, Y) = (X+Y)/2